Cognizione, conoscenza e comunicazione della scienza

Nelle materie di cui mi occupo — la filosofia della scienza e alcuni ambiti delle scienze cognitive — la comunicazione della scienza non è un tema molto presente. Negli ultimi mesi, partecipando alle attività del gruppo di lavoro sulla comunicazione della scienza promosse dalla Fondazione Compagnia di San Paolo di Torino e coordinate dall’Associazione FRAME, sono giunto alla conclusione che questa situazione è in buona parte simmetrica. Nelle discussioni, anche recenti (e a volte piuttosto accese), sulla comunicazione delle scienza, la sua natura e suoi metodi, i riferimenti diretti e specifici alla filosofia della scienza e alle scienze cognitive sono abbastanza rari. Non è detto che questo sia un problema, naturalmente. Credo però che di collegamenti da esplorare meglio ce ne siano diversi, anche a partire da risultati e concetti che in quelle discipline sono considerati classici.

Per scegliere quali esempi presentare qui di seguito, mi sono fatto guidare da due contributi pubblicati nelle ultime settimane. Il primo è stato scritto da Antonio Gomes da Costa, Director of Science Mediation and Education presso Universcience, che riunisce la Cité des Sciences et de l’Industrie e il Palais de la Découverte di Parigi. L’articolo di Gomes da Costa, uscito nel febbraio 2019 su Exsite (la pagina web dello European Network of Science Centres and Museums), offre un punto di vista aggiornato e non scontato su una questione nota e controversa, il ruolo del cosiddetto “deficit model” nell’analisi del rapporto fra i cittadini e le scienze (Gomes da Costa 2019). L’autore del secondo breve scritto che riprenderò più avanti, invece, è proprio un filosofo, e uno dei più influenti in attività: Timothy Williamson dell’Università di Oxford. Per una delle questioni che qui ci interessano, il titolo e il sottotitolo dell’intervento di Williamson (pubblicato dal New Statesman) vanno dritto al punto:

“In the post-truth world, we need to remember the philosophy of science: From climate change to vaccination scares, what non-scientists believe about science is literally a matter of life and death”

Williamson, 2019

L’aeroplano e le interpretazioni naturali

C’è un aeroplano che vola a velocità costante a un’altitudine costante. A un certo punto, lascia cadere una grossa sfera di metallo. Domanda: come è fatta la traiettoria di caduta che la sfera seguirà? All’inizio degli anni Ottanta, lo psicologo sperimentale Micheal McCloskey, insieme ad alcuni collaboratori, pose la stessa domanda a qualche decina di studenti universitari. Il 36% di loro disegnò la traiettoria come nel riquadro D nella Figura 1, seguendo quindi una teoria fisica in cui non vale il principio di inerzia. L’11% delle risposte erano del tipo C: come vanno interpretate? Secondo Paolo Bozzi (Bozzi 1990), la soluzione C “non è altro che la soluzione D immaginata da un ideale soggetto seduto sull’aereo” (p. 37). Così, le risposte “aristoteliche” (che riuniscono appunto la C e la D) riguarderebbero in tutto il 47% dei partecipanti. Anche la risposta B, seguita dal 13% dei partecipanti, ha un elemento “pre-moderno”, perché qui l’effetto dell’inerzia della sfera è previsto, ma la componente verticale del moto è considerata costante. Infine, il 40% dei partecipanti disegnò una traiettoria simile a quella nel riquadro A, approssimativamente parabolica e quindi in linea con la fisica moderna. Fra questi, comunque, risultava talvolta presente l’idea che, al momento dell’impatto al suolo, la sfera si trovasse decisamente indietro rispetto alla posizione raggiunta nel frattempo dall’aeroplano (McCloskey 1983, pp. 302-304).

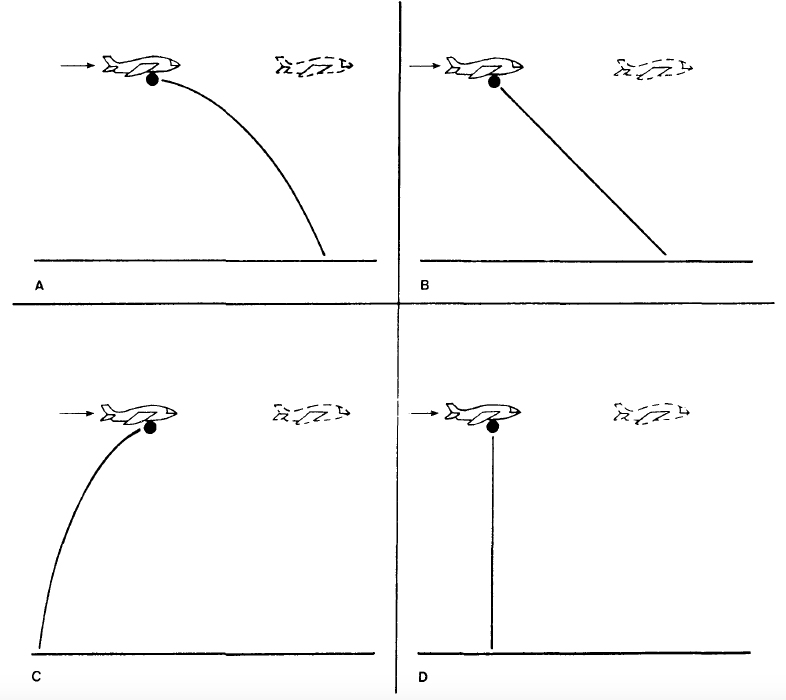
Studi come quelli di McCloskey e collaboratori sulla “fisica ingenua” illustrano un fenomeno molto più generale, che mi pare sia stato sottovalutato non solo dai fautori del cosiddetto “deficit model”, ma anche in molte delle reazioni critiche che sono state rivolte a quell’approccio. Provo a spiegare perché.

Seguendo l’analisi di Gomes da Costa (2019), nelle critiche al deficit model si è osservato (non senza ragione) che “il ‘pubblico’ non è un recipiente vuoto” che vada semplicemente riempito con un travaso di conoscenze scientifiche adeguate. Nel contestare questa idea, gli oppositori del deficit model hanno spesso notato che i non-scienziati possono disporre di conoscenze legittime e pertinenti (“lay knowledge”, “sapere laico”) anche se queste non emergono da un approccio scientifico formale. Seguendo il filo delle metafore, una prospettiva di questo genere suggerisce un “modello della miscela”: ci sarebbero due contenitori entrambi pieni, e le informazioni che contengono (quelle scientifiche e quelle del “pubblico”) si distinguono in modo marcato per origine e struttura. Comunicare la scienza adeguatamente consisterebbe nel  combinare questi due tipi di contenuti senza che nessuno dei due venga svilito o distorto, ma anzi facendoli interagire in modo costruttivo perché ne emerga un livello più avanzato di conoscenza condivisa.

I casi in cui questo schema è effettivamente prevalente (poniamo, alcune questioni di salute pubblica) evidenziano indubbiamente certe mancanze del deficit model e suggeriscono un punto di vista meno asimmetrico e più partecipato alla condivisione dei contenuti scientifici. A mio parere, però, l’illustrazione della fisica ingenua dell’aeroplano indica che, in altri casi, i limiti del deficit model emergono seguendo percorsi decisamente diversi. Di fronte a problemi che il linguaggio delle scienze può formulare e affrontare efficacemente, la mente umana non è un recipiente vuoto — è vero — non per la presenza di contenuti potenzialmente validi, alternativi e compatibili rispetto a quelli scientifici, ma piuttosto perché genera spontaneamente soluzioni intuitivamente plausibili che vanno in direzioni sistematicamente divergenti rispetto alle migliori conoscenze scientifiche disponibili. In mancanza di meglio, chiamerò tali soluzioni intuitive “interpretazioni naturali” (prendendo a prestito il termine, ma adattando l’idea, da Feyerabend 1975).

Le interpretazioni naturali non sono una forma di “conoscenza non scientifica”, perché (detto un po’ brutalmente) normalmente sono false. Tuttavia, vorrei suggerire alcune ragioni per cui meritano una considerazione attenta e specifica che non trova spazio — per motivi in qualche modo opposti e simmetrici — né nel deficit model comunemente inteso né in qualche variante del “modello della miscela”.

Per prima cosa, le interpretazioni naturali non sono affatto estranee alla scienze, e soprattutto alla loro storia. Per molti versi, gli aspetti più straordinari dell’evoluzione delle scienze consistono nel progressivo e ricorrente superamento di interpretazioni naturali (un processo che risale almeno all’epoca di Platone e Aristotele). Il caso della polemica di Galileo con “gli aristotelici” a proposito dell’“argomento della torre” e il moto della Terra (Feyerabend 1975 ne dà appunto una ricostruzione classica) è un ottimo esempio, ma non è l’unico né il più antico. Quando frenano l’assimilazione e la comprensione di contentuti scientifici contemporanei, quindi, le interpretazioni naturali spesso ripetono su piccola scala frammenti della storia della disciplina in questione. Ne consegue che una conoscenza non superficiale della storia di una data scienza è uno strumento rilevante per una comunicazione efficace dei suoi contenuti — uno strumento, occorre aggiungere, che gli stessi esperti normalmente non ricevono con la loro formazione.

Gli scienziati di ieri hanno avuto bisogno, per far crescere la scienza, di scoprire (spesso con notevole fatica) che cosa c’era di sbagliato in certe interpretazioni naturali. Almeno idealmente, quindi, comunicare la scienza ai cittadini (non-scienziati) di oggi implica che venga loro offerta la stessa opportunità. Ma allora, nella prospettiva che suggerisco, atteggiamenti di disinteresse, stupore o accondiscendenza da parte degli esperti — che possono emergere in modo fin troppo spontaneo — sono senz’altro da evitare, anche se per motivi diversi, tanto quanto lo sono nei casi in cui vi siano elementi reali di “conoscenza laica” e non scientifica. La considerazione esplicita delle interpretazioni naturali e del loro ruolo fornisce in effetti una forte motivazione per comunicare la scienza non solo come insieme di contenuti ma anche il più possibile come processo di elaborazione di quei contenuti. Anche qui si tratta, vorrei notare, di una motivazione distinta e specifica rispetto ad altre (usuali e pure legittime) che dipendono, poniamo, dalla rilevanza ed efficacia dello story-telling nella comunicazione.

Infine, le interpretazioni naturali sono, appunto, naturali: la loro presenza è tendenzialmente prevedibile e pervasiva. Per suggerire che è così, mi sono servito di un singolo esempio classico che riguarda la fisica ingenua (una discussione più recente si trova in Kubricht, Holyoak e Hongjing 2017), ma è mia opinione che il fenomeno si manifesti negli ambiti disciplinari più svariati (si veda Carlisle e Shafir 2005 per un esempio di tipo differente). Può capitare che le interpretazioni naturali restino presenti persino nel lavoro degli esperti: si pensi alla questione dei veri o presunti residui finalistici in discussioni teoriche di biologia evoluzionistica, di come sia complicato identificarli e neutralizzarne gli effetti. A maggior ragione, quindi, dobbiamo aspettarci che le interpretazioni naturali siano all’opera quando un esperto della disciplina X si trova a ragionare a proposito di una diversa disciplina Y. Ah, e ai fini della discussione che propongo qui anche lo studio della comunicazione della scienza è una disciplina scientifica! (Che poi sia una disciplina difficile e acerba, è un’altra questione.)

La mano di carte e il ragionamento fallibile

State giocando con il vostro amico Luca una partita a carte molto combattuta, e vi farebbe comodo sapere se ha in mano un asso. Considerate le due seguenti proposizioni e immaginate di sapere che solo una delle due è vera (non sapete quale, però); l’altra invece è falsa.

1. Se nella mano di carte di Luca c’è un re, allora c’è un asso.
2. Se nella mano di carte di Luca non c’è un re, allora c’è un asso.

Che cosa potete concludere?
A. Nella mano di carte di Luca c’è un asso.
B. Nella mano di carte di Luca non c’è un asso.
C. Nella mano di carte di Luca potrebbe esserci o non esserci un asso.

Questo problema è stato ideato dagli psicologi cognitivi Phil Jonhson-Laird e Fabien Savary una ventina d’anni fa (Jonhson-Laird e Savary 1999). Si tratta di un compito di ragionamento, per così dire, puro: non ha praticamente niente a che fare con quello che sappiamo o non sappiamo di questioni scientifiche, storiche o di altro genere. Che cosa hanno scoperto Jonhson-Laird e Savary? Che la maggioranza delle persone sceglie la risposta A. (Voi che cosa avete scelto?) Questa risposta, però, è sbagliata.
Perché? In breve, la spiegazione è questa. Supponiamo che nella mano di Luca ci sia effettivamente un re, e inoltre che la proposizione falsa sia (1): allora non possiamo concludere che nella mano c’è un asso; potrebbe benissimo non esserci. (Lo stesso vale se nella mano non c’è un re e la proposizione falsa è la (2))1. Semplice, no?

Se pensate che il problema logico della mano di carte sia un rompicapo che interessa solo qualche curioso, la state facendo troppo facile. Ho scelto questo esempio perché relativamente veloce da raccontare e meno noto di altri, ma la tradizione di studi a cui appartiene ha prodotto una gran quantità di risultati con una morale molto chiara: la razionalità degli umani è profondamente limitata e imperfetta. È vero, le persone se la cavano bene ragionando per scorciatoie (“euristiche”, nella terminologia scientifica) nella maggior parte dei casi. Ma quando è necessario seguire i principi logici più rigorosi del ragionamento, le sbandate sono frequenti e sistematiche, persino se — questo è importante — le informazioni fattuali necessarie ci sono tutte e nulla di estraneo interferisce con la nostra concentrazione. (Fra i molti possibili, è d’obbligo almeno il riferimento a Kahneman 2012.)

L’errore nel problema delle carte è un’“illusione logica” con le stesse caratteristiche di altri fenomeni ben noti, il più famoso dei quali è forse il cosiddetto “bias di conferma” (che in realtà è una serie di meccanismi cognitivi connessi ma distinti, si veda Nickerson 1998). Ora, gli errori cognitivi si chiamano così perché emergono da schemi di ragionamento universalmente diffusi. Non c’è dubbio che vi siano importanti interazioni fra i contenuti contingenti di cui le persone dispongono e i percorsi cognitivi che seguono (non a caso, anche queste interazioni sono temi di ricerca molto studiati). Ma, per quanto ne sappiamo, non c’è nessuna conoscenza di dominio che di per sé neutralizzi la suscettibilità alle distorsioni sistematiche del ragionamento. In effetti, le scienze hanno prodotto i loro esiti più spettacolari non perché fra gli scienziati i bias cognitivi magicamente svaniscano, ma piuttosto a dispetto della loro persistenza. Le scienze rappresentano il paradigma della razionalità proprio perché hanno messo a punto una collezione di procedure e accortezze che mirano a ridurre gli errori che possono emergere da intuizioni fuorvianti e trabocchetti logici (il paradigma di tali procedure sono, naturalmente, la dimostrazione matematica e la sperimentazione controllata).

Che cosa c’entra questo con il deficit model e la comunicazione della scienza? Per vederlo, torniamo a Gomes da Costa (2019). Secondo l’autore, l’attacco al deficit model è stato in parte influenzato da un equivoco: si è dato spesso per scontato che il modello prescrivesse il riempimento di un vuoto (il deficit) di informazioni fattuali, che sarebbero ignorate dal pubblico. In realtà, osserva Gomes da Costa, già nel cosiddetto “Bodmer report” (Royal Society of London, The Public Understanding of Science, 1985) c’era grande attenzione alla necessità di diffondere presso il pubblico la consapevolezza di fondamentali elementi di metodo che guidano la produzione e la valutazione dei contenuti delle scienze. Se recuperiamo questo aspetto — è una delle conclusioni dell’articolo — il deficit model può mantenere un ruolo significativo nell’analisi e nella progettazione di interventi. In questo modo, però, il presupposto che “esista un gruppo che detiene le conoscenze e le abilità considerate essenziali per comprendere il mondo e far fronte alle sfide contemporanee, e un altro gruppo che non le ha” (Gomes da Costa 2019) resta intatto, solo che ora la trasmissione da un gruppo all’altro comprende aspetti di metodo oltre che informazioni fattuali. Come abbiamo già visto, nel “modello della miscela” questo presupposto è contestato in modo diretto, rivendicando come il “pubblico” avrebbe accesso a conoscenze di un tipo specifico al di fuori dell’ambito delle scienze. Ma anche in questo caso mi pare ci siano altre ragioni, distinte e  indipendenti, per ripensare una divisione così netta: individui esperti e non esperti sono accomunati da strutture cognitive qualitativamente affini, generalmente efficienti ma anche inclini a errori sistematici (Jeng 2006 offre una discussione interessante), e i principi metodologici distintivi dell’indagine scientifica sono per lo più “innaturali” per gli uni come per gli altri. In questo, in effetti, sta molta della loro importanza.

La prefazione: conoscenza e incertezza

La Prof.ssa K. è una studiosa capace, rigorosa e stimata. Si occupa di storia medievale, e ha raccolto i risultati delle sue ricerche degli ultimi anni in un libro. Il testo è voluminoso e contiene 100 tesi distinte — chiamiamole T1, T2, …, T100 — di notevole importanza scientifica. Nel libro della Prof.ssa K., ciascuna delle 100 tesi è sostenuta da argomenti che partono da premesse accertate (per esempio, relative a documenti effettivamente accessibili). Le argomentazioni per ciascuna delle tesi T1,
…, T100 non sono infallibili (come, poniamo, delle dimostrazioni matematiche), ma sono comunque molto forti. Per questi motivi, nella Prefazione al suo lavoro, la Prof.ssa K. scrive “per ciascuna delle tesi che presento, sono convinta che sia vera in base ai dati disponibili”. “D’altra parte”, aggiunge però K., “ritengo anche probabile che almeno una fra esse sia falsa”.

1. Quale fra queste due opposte asserzioni consideri più convincente?
1a. Ciò che K. scrive nella Prefazione non ha senso: è incoerente.
1b. Ciò che K. scrive nella Prefazione è perfettamente sensato e coerente.
2. Quale fra queste due opposte asserzioni consideri più convincente?
2a. Il libro di K. conterrà probabilmente molte vere conoscenze.
2b. Il libro di K. non può contenere nessuna vera conoscenza.

Diversamente dagli esempi usati in precedenza, quello della Prefazione non viene da studi di psicologia sperimentale. L’ho adattato da un famoso “paradosso” (si chiama, appunto, il paradosso della prefazione), molto noto nell’epistemologia contemporanea (Clark 2002, pp. 189-191). Inoltre, non ci sono risposte completamente pacifiche per le domande 1 e 2 più sopra. Nella parte finale di questo contributo, intendo suggerire tre cose: (i) come e perché è plausibile la combinazione delle risposte più “ottimistiche”, cioè 1b e 2a; (ii) che l’esempio della prefazione è, almeno per i nostri scopi, un’utile metafora di tutta la scienza; e (iii) che illustra bene certi concetti filosofici centrali e utili per comunicare la scienza.

Prima di arrivare ai punti (i)-(iii), però, dovrò ampliare un po’ il discorso. Prometto che l’apparente (breve) divagazione non sarà inutile.

Provate a chiedere a un fisico se è vero quello che le teorie fisiche dicono a proposito degli elettroni. È facile che vi risponda qualcosa del genere: “In che senso ‘vero’? Il formalismo che contiene il termine ‘elettrone’ produce previsioni sperimentalmente controllabili e molto accurate. Se è questo che intendiamo, allora sì, è ‘vero’. Ma di più non possiamo dire.” Se fate una domanda simile a un matematico, le risposte più frequenti saranno di due tipi diversi. La prima è, più o meno, questa: “Io credo che gli enunciati matematici siano veri perché descrivono entità eterne e astratte. Ma si tratta di una credenza indimostrata e indimostrabile: una fede intuitiva!” La seconda invece (forse leggermente meno popolare, ma per alcuni molto convincente) suona così: “Non ha senso dire che gli enunciati della matematica sono veri o falsi, perché non descrivono niente che faccia parte del mondo materiale. La matematica è come un gioco molto speciale: produce metodi di manipolazione di simboli conformi a regole rigorose, e basta.” Questi esempi sono paradigmatici, ma di certo non gli unici: gli esperti di una certa disciplina, di solito, hanno un abbozzo di filosofia della loro scienza (e vale anche per le scienze umane). Secondo l’efficace formulazione di Daniel Dennett, “non esiste scienza del tutto indipendente dalla filosofia, ma solo scienza praticata senza considerazione per i suoi assunti filosofici fondamentali” (Dennett 2013, pp. 19-20). In effetti, tutte le risposte più sopra presentano sommariamente posizioni teoriche già formulate in modo sofisticato decenni (a volte secoli) fa, che in filosofia sono state ampiamente discusse, criticate, rielaborate e migliorate. Potremmo chiamarle “filosofie delle domenica”, perché forniscono a un esperto una risposta sintetica e plausibile a quesiti che normalmente sono estranei all’attività quotidiana nei dipartimenti e nei laboratori (quesiti che a volte vengono proprio da qualche scocciatore curioso in un contesto inusuale, come appunto un filosofo o magari un giornalista). Ma dato che “filosofie della domenica” suona un po’ irriverente, userò l’etichetta più neutrale di “filosofie ancillari”.

Normalmente, chi si occupa di comunicazione della scienza ha ricevuto una formazione scientifica (di nuovo: le scienze umane sono comprese), e quindi ha familiarità con
almeno qualche elemento di filosofia ancillare della scienza. Come detto, le filosofie ancillari hanno una funzione “di servizio” (epistemologica e psicologica) rispetto ai membri di una comunità disciplinare. Proprio per questo, però, non sono state definite come una base teorica adatta per sostenere attività e progetti di comunicazione della scienza. Prendiamo un esempio. A mio parere, un problema filosofico centrale per i dibattiti recenti sulla comunicazione della scienza è la possibile conciliazione fra conoscenza e incertezza. In molte società contemporanee, infatti, la fallibilità della scienza (che anche la sua storia in qualche misura illustra) è un dato culturalmente acquisito, che va riconosciuto e anzi chiarito. Dall’altra parte, le scienze sono ancora considerate come fonti di conoscenza straordinarie e insostituibili per la comprensione del mondo e l’orientamento delle scelte individuali e sociali — una percezione pienamente motivata che rappresenta anche un capitale sociale da preservare. Esiste una visione teorica coerente che tenga insieme queste due idee? Cercare di derivare una risposta dalle filosofie ancillari non è una mossa molto promettente, secondo me: per le ragioni elencate prima, i loro elementi non hanno le giuste caratteristiche di rilevanza e generalità. E questo ci riporta all’articolo di Williamson (2019), e all’esempio della Prefazione.

Williamson sottolinea la necessità di tenere ferma la distinzione fra tre elementi fondamentali: la realtà, i dati, e le teorie. Seguendo la sua illustrazione (che fa riferimento al cambiamento climatico):

“Accurate, effective reporting of science must be honest about the nature of the scientific arguments without losing the reader in technicalities. Achieving even an elementary understanding of the science requires distinguishing three dimensions: its subject (such as the past, present, and future climate), evidence about the subject (such as measurements of temperature), and theories about it (such as a hypothetical mechanism for global warming). To confuse any two of these three dimensions leads to alarming mental muddles, in which no theory lacks evidence, or nothing happens unobserved, or a change of theory is a change of climate.”

Williamson, 2019

Ora facciamo un passo in più. I dati sostengono (con maggiore o minore forza) l’accettazione delle teorie: nella terminologia epistemologica tradizionale, si tratta della relazione logica di giustificazione. La verità o falsità delle teorie, invece, dipende esclusivamente dal rapporto fra teoria e realtà: la prima può descrivere (più o meno accuratamente) la seconda, oppure no, e non fa nessuna differenza che cosa noi crediamo e perché. Ne consegue che giustificazione e verità non sono la stessa cosa. E la conoscenza? Secondo la tradizione, è una credenza (in una teoria) vera (che corrisponde alla realtà) e giustificata (dai dati). È un’analisi della conoscenza che i filosofi discutono nei dettagli da un paio di millenni, ma per quello che ci interessa qui andrà benissimo così com’è.

Sembra tutto troppo semplice? Nel suo articolo, Williamson non nasconde di certo come il lavoro della ricerca filosofica (compreso il suo: Williamson 2000) abbia prodotto molte varianti e importanti precisazioni di questo schema essenziale (Marconi 2007 è un buon punto di partenza per approfondire un po’). Ma ricordiamo qual è il nostro scopo, tutto sommato modesto: ci chiediamo se sia possibile tratteggiare un’interpretazione generale che tenga insieme le idee di conoscenza e di incertezza, facendo così fronte ad alcune esigenze di fondo della comunicazione della scienza — un proposito che normalmente non si pongono (e in effetti non conseguono) quelle che ho chiamato filosofie ancillari.

Torniamo quindi alla protagonista della nostra storia immaginaria, la Prof.ssa K., che ha 100 ipotesi, ciascuna sostenuta con forza dai dati disponibili e rilevanti. K. non può escludere completamente di sbagliarsi, ma considera ognuna delle sue ipotesi molto probabile in base ai dati, e così di ciascuna crede che sia vera. Dato però che sono tante (e distinte), anche la probabilità che almeno una fra T1, T2, …, T100 sia falsa è significativa (semplificando un po’, è una grande somma di tante piccole probabilità), e K. ne è al corrente. Se è così, si capisce il senso di quello che K. scrive nella sua Prefazione: abbiamo quindi una ricostruzione della situazione in accordo con la risposta 1b. Bene. Ma possiamo anche dire che il libro di K. contiene molte conoscenze? (Questa è la risposta 2a.) In fondo, uno potrebbe obiettare, per ciascuna delle ipotesi T1, T2, …, T100 presa singolarmente non possiamo escludere che sia falsa. Attenzione, però: abbiamo buone ragioni (l’insieme dei dati disponibili) per ritenere che parecchie di quelle tesi siano vere. Infatti abbiamo appena detto che (in base ai dati rilevanti) ciascuna è molto probabile! Allora, le tesi di K. sono credenze giustificate, e molte saranno vere; e così, molte soddisfano la definizione usuale di conoscenza. Non sappiamo con certezza quali esattamente, ma resta perfettamente sensato ritenere che fra T1, T2, …, e T100 ci siano effettivamente molte conoscenze.

Ecco, in un certo senso, le scienze nel loro insieme sono come il libro della Prof.ssa K. Per ciascuno dei loro contenuti più avanzati e importanti (ipotesi e teorie), indubbiamente esiste la possibilità che sia falso e quindi esiste anche la possibilità (enormemente più remota) che tutti siano falsi (Popper, per esempio, lo ha sottolineato esplicitamente: “tutta la scienza potrebbe sbagliare”, Popper 1935/1959, p. 7). Ma non siamo affatto costretti a supporre che la conoscenza richieda assoluta certezza. Nei termini che abbiamo adattato da Williamson (2019), la cosa più ragionevole da pensare è che fra le nostre ipotesi sostenute dai dati molte siano effettivamente vere, e siano quindi una base solida per interpretare il mondo e guidare l’azione. Insomma, conoscenza e incertezza non si contraddicono. QED.

1. Una volta esclusa A, è naturale pensare che la risposta corretta sia C. Si tratta di una conclusione ragionevole per molte interpretazioni plausibili delle proposizioni (1) e (2). Per essere precisi, però, la faccenda è più complicata. Se interpretiamo (1) e (2) alla luce del connettivo condizionale della logica proposizionale classica, allora l’unica risposta corretta (per quanto possa sembrare innaturale) è proprio la B. Infatti, utilizzando questa interpretazione di “se… allora…”, un enunciato condizionale è sempre vero, a meno che non sia vero l’antecedente ma falso il conseguente. Così, la presenza di un asso nella mano di Luca renderebbe immediatamente vere sia (1) sia (2). Ma sappiamo invece che una sola è vera, quindi l’asso non può esserci. Dopodiché, se nella mano c’è un re, (1) sarà falsa e (2) vera; altrimenti, il contrario.